with SpcAudace?
Page updated the 2011-11-08

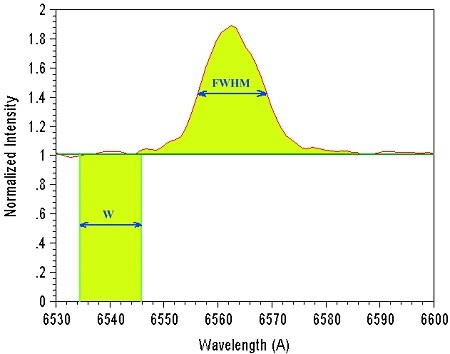
What is the equivalent width (EW)?:
EW is used in any application where you need to know the the strength of a line.
EW's definition is:
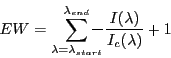
I(λ) : spectrum's intensity at wavelength λ
Ic(λ) : continuum's intensity at wavelength λ
EW<0 for emission lines, as done with MIDAS.Theoretically, resolution should have no effect in EW because of the way it is measured.
EW's computation needs continuum's intensities Ic which can be extracted from spectrum by several ways. So, it seems that there is no need to normalize the spectrum.
We have found the following criteria that should impact on EW's computation:
- Wavelength bandwidth for integration;
- Continuum extraction method;
- Star's behaviour of course;
- For the same date, EW depends on the observer (experimental bias, spectral reduction, ...);
- Depends on software's version (id. algorithm used for computation).

The easiest way is calling spc_autoew command:
- Looking for the command synthax: spc_autoew
# Usage: spc_autoew nom_profil_raies lambda_raie/lambda_deb lambda_fin ?taux_doucissage_continuum (0-[6]-15)?- Let Spcaudace find limits wavelengths: spc_autoew zet_tau_20100414.fit 6563
6563 is the approximate Halpha wavelength, found limits appear in Audela's Console:
# Date: 2010-04-14T20:55:04.99
# JD: 2455301.372
# EW(83.54=6548.52-6632.06)=-15.42 A.
# Sigma(EW)=0.67 A.
# SNR=199.- You know what are wavelength limits: spc_autoew zet_tau_20100414.fit 6535 6595
# Date: 2010-04-14T20:55:04.99
# JD: 2455301.372
# EW(60.0=6535.0-6595.0)=-14.82 A.
# Sigma(EW)=0.5 A.
# SNR=199.
We can see that extracted continuum produced with default options fits star continuum rather well on this zeta Tau spectrum:
Spcaudace computes uncertainty for each EW run. It's available in Audela's Console: Sigma(EW)=0.5 A.
You can adjust continuum smoothing with a power of 10 given as a new command parameter.
Command: spc_autoew zet_tau_20100414.fit 6535 6595 8Output:
# Date: 2010-04-14T20:55:04.99
# JD: 2455301.372
# EW(60.0=6535.0-6595.0)=-14.18 A.
# Sigma(EW)=0.5 A.
# SNR=199.

Different ways to do continuum extraction:
1. How to choose a continuum?
Depending on parameters given to spc_ew command, extracted continuum will fit or not star's continuum and EW value may be different. We can see bellow few continuum extracted from the same star and the EW obtained with it on this CI Cyg spectrum. Operator has to watch how continuum is fitted in order to choose the best way.
Continuum has a great impact on EW's value. So whitch continuum is the best?
Here after parameters available to control continuum fiting ("o" means yes, ?? means optional arguments):
spc_ew lines_profile_file_name lamba_begin lambda_end ?continuum_smooth_rate (0-[6]-15)? ?overplot_continuum(o/n)? ?continuum_polynom_order(2)?
spc_ew nom_profil_raies_calibre lamba_debut lambda_fin ?taux_doucissage_continuum (0-[6]-15)? ?superposer_continuum(o/n)? ?degre_polynomes_continuum_methode_pbas(2)?With this star, the last try, i.e. multi linear pieces smoothed with factor 10^6 seems to be the best continuum fitting which takes care of global slop of left edge and right edge stellar's continuum and that has the smallest curvature.
When last command argument equal to 0, continuum used for EW computation is a constant equal to 1. But it's a bad idea in many cases.
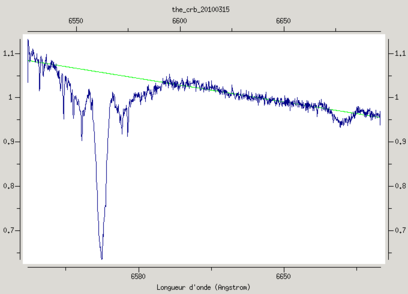
But with an other star (theta Crb spectrum), low pass filter with deg 2 polynom would be the best.Command: spc_ew the_crb_20100315.fit 6535 6595 6 n 2
2. How to do with low SNR spectra?
Continuum extraction's main difficulty comes from continuum's SNR. In the last example (CI Cyg spectrum), SNR was very low and algorithms have few possibilities how to find continuum median position in wide spread distribution of intensities.
Command: spc_ew ci_cyg_20100903_905 6535 6595 6 n 2
Output: # Date: 2010-09-03T21:43:08.98
# JD: 2455443.405
# EW(60.0=6535.0-6595.0)=-168.05 A.
# Sigma(EW)=81.29 A.
# SNR=3.

Possible work after continnum's extraction method is defined for a star:
So, before beginning before launching a time study of EW's evolution, it is needed to select the more adapted method for continuum extraction witch depends on the star. After what a pipeline may be applyed.
Here is an example of such pipeline for EW time evolution:
spc_ewcourbe arguments are (?? means optional arguments): spc_ewcourbe lambda_begin lambda_end ?polynome order(default is 1)?
spc_ewcourbe lambda_raie/lambda_deb lambda_fin ?degre polynome du continuum(1)?A periodogramm (spc_periodogram SpcAudace command) may resolve the period too if there are anougth points (ewcourbe_20100421.dat):
Command: spc_periodogram ewcourbe_20100421.dat "julian days" EWOutput:
# le fichier periodogram.dat a ete cree
# Export Gnuplot (0=OK) : 0
# Graphique sauve sous periodogram.png
# Le nombre de maxima 4 trouves est inferieur au nombre demande
# Maximum No1 trouve pour une periode de 32.6478882814 avec une valeur de 4.5788506286
# Maximum No2 trouve pour une periode de 21.1286335938 avec une valeur de 1.29110733541
# Maximum No3 trouve pour une periode de 14.249078711 avec une valeur de 0.809717495148
# Maximum No4 trouve pour une periode de 9.76936855472 avec une valeur de 0.75780796022